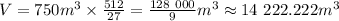Question

PLEASE HELP!!!

the surface area of two similar solids are 45cm^2 and 320cm^2. 1: what is the scale factor? 2; what is the ratio of their volume and 3: if the volume of the smaller solid is 750m^3. what is the volume of the larger solid?

Answer 1

`\frac83; (512)/(27); 14\ 222.222 m^3`

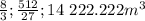
Explanation:

In general, if in two similar solids the corrisponding linear measure (same side, same diagonal, etc) are in a ratio of K, surface measures will be in a ratio of
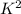`K^2` and volumes will be in a ratio of
`K^3`. We know the ratio of the surfaces, so we can say that

`K^2 = (320)/(45) = \frac{64}9`

1. the ratio of the scale factor can be easily found by the ratio of the surfaces, and it's
`K= √(K^2) = \sqrt{(64)/(9)} = \frac83`

2. The ratio of the volumes is the cube of the ratio we just found:

`K^3 = (\frac83)^3 =(512)/(27)`

3. to find the volume of the larger solid you just multiply the ratio we found in the last point by the volume of the smaller solid.

`V=750m^3* (512)/(27) = (128\ 000)/(9) m^3 \approx 14\ 222.222 m^3`