The opening of a tunnel that travels through a mountainside can be modeled by y = - \frac {2}{15} (x - 15)(x + 15), where x and y are measured in feet. The x-axis represents the…

Question

asked Aug 17, 2021 32.6k views

1 Answer

Nyps · Answer 1 · 2021-08-24T15:34:20+0000

Answer:

(a) 30 feet

(b) 30 feet.

Explanation:

Given that the opening of a tunnel that travels through a mountainside can be modeled by

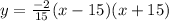y=(-2)/(15) (x-15)(x+15) , where x and y are measured in feet.

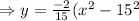
$\Rightarrow y=(-2)/(15)(x^2-15^2}$

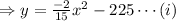
$\Rightarrow y=(-2)/(15){x^2-225}\cdots(i)$

(a) At the ground level,
y=0

So, the width of the tunnel at ground level is distance between the extreme point of the tunnel on the grount.

For,
y=0 , the extreme points of the tunnel.

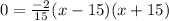
0=(-2)/(15) (x-15)(x+15)

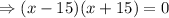
$\Rightarrow (x-15)(x+15) =0$

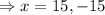
$\Rightarrow x= 15, -15$

So, the extreme points of the tunnel are,
x_1=15 and
x_2=-15 .

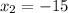Hence, the width of the tunnel at the ground level

= | x_1 - x_2 |

=|15-(-15)|

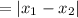
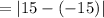
=30 feet.

(b) The maximum height of the tunnel can be determiment by determining the maxima of the given function.

First determining the value of x for which the slope of the graph is zero.

(dy)/(dx)=0

From equation (i),

-2x=0

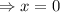
$\Rightarrow x=0$

And
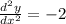
(d^2y)/(dx^2)= -2

which is always negative, so at x=0 the value of y is maximum.

Again, put x=0 in equation (i), we have

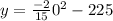
$y=(-2)/(15){0^2-225}$

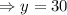$\Rightarrow y=30$ feet.

Hence, the tunnel is 30 feet tall.