Question

Sulfur dioxide and oxygen react to form sulfur trioxide during one of the key steps in sulfuric acid synthesis. An industrial chemist studying this reaction fills a 50.0L tank with 14. mol of sulfur dioxide gas and 2.6 mol of oxygen gas, and when the mixture has come to equilibrium measures the amount of sulfur trioxide gas to be 1.6 mol. Calculate the concentration equilibrium constant for the reaction of sulfur dioxide and oxygen at the final temperature of the mixture. Round your answer to 2 significant digits.

Answer 1

Step-by-step explanation:

From the given information:

The equation for the reaction can be represented as:

`2SO_2 + O_2 \to 2SO_3`

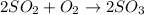
The I.C.E table can be represented as:

2SO₂ O₂ 2SO₃

Initial: 14 2.6 0

Change: -2x -x +2x

Equilibrium: 14 - 2x 2.6 - x 2x

However, Since the amount of sulfur trioxide gas to be 1.6 mol.

SO₃ = 2x,

then x = 1.6/2

x = 0.8 mol

For 2SO₂; we have 14 - 2x

= 14 - 2(0.8)

= 14 - 1.6

= 12.4 mol

For O₂; we have 2.6 - x

= 2.6 - 1.6

= 1.0 mol

Thus;

[SO₂] = moles / volume = ( 12.4/50) = 0.248 M ,

[O₂] = 1/50 = 0.02 M ,

[SO₃] = 1.6/50 = 0.032 M

Kc = [SO₃]² / [SO₂]² [O₂]

= ( 0.032²) / ( 0.248² x 0.02)

= 0.8325

Recall that; the equilibrium constant for the reaction
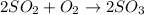`2SO_2 + O_2 \to 2SO_3` = 0.8325;

If we want to find:

`SO_2 + (1)/(2)O_2 \to SO_3`

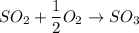
Then:

`K_c = (0.8325)^(1/2)`

`\mathbf{K_c = 0.912}`

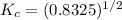
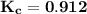
Since no temperature is given to use in the question, it will be impossible to find the final temperature of the mixture.