Answer:
The leading coefficient is 3
Explanation:
Polynomials
Given the roots of a polynomial x1,x2,x3, it can be expressed as:

Where a is the leading coefficient.
We are given the roots x1=-6, x2=7i, x3=-7i, thus:
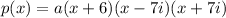
Operating the product of the conjugated imaginary roots:
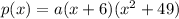
Knowing p(2)=1,272 we can find the value of a
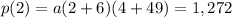
Operating:
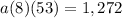
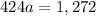
Solving:
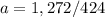
a=3
The leading coefficient is 3