Question

What is the leading coefficient of a third degree polynomial function that has an output of 1,272 when x=2, and has zeros of −6, 7i, and −7i?

Answer 1

The leading coefficient is 3

Explanation:

Polynomials

Given the roots of a polynomial x1,x2,x3, it can be expressed as:

`p(x)=a(x-x1)(x-x2)(x-x3)`

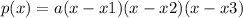
Where a is the leading coefficient.

We are given the roots x1=-6, x2=7i, x3=-7i, thus:

`p(x)=a(x+6)(x-7i)(x+7i)`

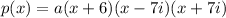
Operating the product of the conjugated imaginary roots:

`p(x)=a(x+6)(x^2+49)`

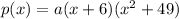
Knowing p(2)=1,272 we can find the value of a

`p(2)=a(2+6)(4+49)=1,272`

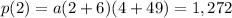
Operating:

`a(8)(53)=1,272`

`424a=1,272`

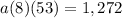
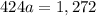
Solving:

`a=1,272/424`

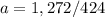
a=3

The leading coefficient is 3