Question

Write a factor that you can use to rationalize the denominator of $\frac{\sqrt{2}}{\sqrt{5}-8}$

Answer 1

`√(5)+8`

Explanation:

To rationalize the denominator, you would need to multiply the numerator and denominator by its conjugate. The conjugate of
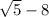`√(5)-8` is
`√(5)+8`, so, if you wanted to do the actual math:

`\displaystyle (√(2))/(√(5)-8)\\ \\(√(2))/(√(5)-8)\cdot(√(5)+8)/(√(5)+8)\\ \\(√(10)+8√(2))/(5-64)\\ \\(√(10)+8√(2))/(-59)\\ \\(√(10)-8√(2))/(59)`

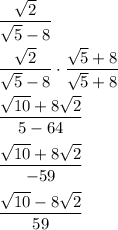
This method works because
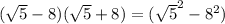`(√(5)-8)(√(5)+8)=(√(5)^2-8^2)`, which is a difference of squares, and helps to eliminate the radicals in the denominator.

Hope this helps!

Answer 2

hello.

The rationalizing factor of it is root 2/root 5+8

We must multiply both numerator and denominator by it.