Answer: (a) B = 2 x 10⁻⁵T
(b) B = 1.94 x 10⁻⁵T
(c) B = 1.8 x 10⁻⁴T
Step-by-step explanation: A magnetic field due to a current passing through a straight wire is calculated using the Biot-Savart Law:
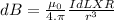
where
dL is current length element
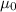 is permeability of free space (
is permeability of free space (
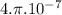 T.m/A)
T.m/A)
(a) For a infinite straight wire:
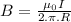
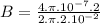
B = 2x10⁻⁵T
For an infinite, long and straight wire, magnetic field is 2x10⁻⁵T.
(b) For a finite wire:
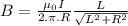
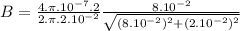
B = 1.94x10⁻⁵T
The magnetic field for a finite wire in the same conditionsas infinite wire is 1.94x10⁻⁵T.
(c) For a finite wire at a point distant from the end of the wire:
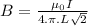
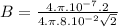
B = 0.18x10⁻⁵T
At a point at the end, magnetic field is 1.8x10⁻⁴T.