Question

Activity Problem 8.3 This problem asks you to compare the finite current element approximation to the infinite straight wire approximation for the isolated segment of wire carrying current of 2A to the right. The wire is 8cm long. Note, the finite current approximation will be a fairly poor approximation to the actual field which would be found by integration; the infinite wire field is a better approximation in this case. (a)Compute the magnetic field at point C a distance 2cm for the center of the wire using the infinite straight wire approximation. (b)Compute the magnetic field at point C using the finite current element approximation. (c)Compute the magnetic field at point E a distance 2cm from the end using the finite current element approximation.

Answer 1

Answer: (a) B = 2 x 10⁻⁵T

(b) B = 1.94 x 10⁻⁵T

(c) B = 1.8 x 10⁻⁴T

Step-by-step explanation: A magnetic field due to a current passing through a straight wire is calculated using the Biot-Savart Law:

`dB=(\mu_(0))/(4.\pi) (IdLXR)/(r^(3))`

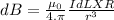
where

dL is current length element

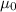`\mu_(0)` is permeability of free space (
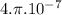`4.\pi.10^(-7)`T.m/A)

(a) For a infinite straight wire:

`B=(\mu_(0)I)/(2.\pi.R)`

`B=(4.\pi.10^(-7).2)/(2.\pi.2.10^(-2))`

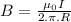
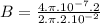
B = 2x10⁻⁵T

For an infinite, long and straight wire, magnetic field is 2x10⁻⁵T.

(b) For a finite wire:

`B=(\mu_(0)I)/(2.\pi.R)\frac{L}{\sqrt{L^(2)+R^(2)} }`

`B=(4.\pi.10^(-7).2)/(2.\pi.2.10^(-2)) \frac{8.10^(-2)}{\sqrt{(8.10^(-2))^(2)+(2.10^(-2))^(2)} }`

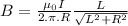
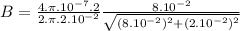
B = 1.94x10⁻⁵T

The magnetic field for a finite wire in the same conditionsas infinite wire is 1.94x10⁻⁵T.

(c) For a finite wire at a point distant from the end of the wire:

`B=(\mu_(0)I)/(4.\pi.L√(2) )`

`B=(4.\pi.10^(-7).2)/(4.\pi.8.10^(-2)√(2) )`

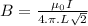
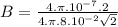
B = 0.18x10⁻⁵T

At a point at the end, magnetic field is 1.8x10⁻⁴T.