Question

In the game of​ roulette, a player can place a ​$ bet on the number and have a probability of winning. If the metal ball lands on ​, the player gets to keep the ​$ paid to play the game and the player is awarded an additional ​$. ​ Otherwise, the player is awarded nothing and the casino takes the​ player's ​$. What is the expected value of the game to the​ player? If you played the game 1000​ times, how much would you expect to​ lose?

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

a

The expected amount to be lost is 0.5263 cents per game

b

The expected amount to be lost is

`P = \$ 526 .3`

Explanation:

From the question we are told that

The probability of winning is
`p = (1)/(38) = 0.0263`

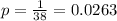
Generally the probability of losing is mathematically evaluated as

`q =  1-p`

=>
`q = 1-0.0263`

=>
`q = 0.9737`

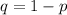
Generally the expected value is mathematically represented as

`E(X) =  \sum x_i *  P(x_i)`

Here
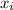`x_i` is a discrete variable (i.e it is a countable ) are outcomes of the player winning and the player losing

So

`E(X) =   x_1 *  P(x_1) + x_2 *  P(x_2)`

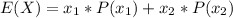
Now the outcome of winning is making $350 so

`x_1 = \$ 350`

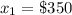
the outcome of losing is losing $10 so

`x_2 = - \$10`

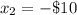
So

`E(X) =  350* 0.0263 -10 *  0.9737`

`E(X) = -0.5263`

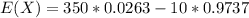
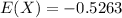
hence the expected amount to be lost is 0.5263 cents per game

If you played the game 1000​ times, the amount that is expected to be lost is

`P =  1000 * -0.5263`

=>
`P = -\$ 526 .3`

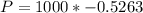
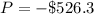
Hence the expected amount to be lost is

`P = \$ 526 .3`