Answer:
58.32 N
Step-by-step explanation:
Area of a circle =


where r is the radius of the circle.
The cylinder has a radius of 0.02 m, its area is;
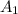 =
=


=
 x
x

=
 x 0.0004
x 0.0004
= 1.2571 x

Area of the cylinder is 0.0013
 .
.
The safety valve has a radius of 0.0075 m, its area is;
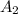 =
=


=
 x
x
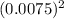
=
 x 5.625 x
x 5.625 x
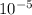
= 1.7679 x
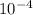
Area of the valve is 0.00018
 .
.
From Hooke's law, the force on the safety valve can be determined by;
F = ke
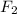 = 950 x 0.0085
= 950 x 0.0085
= 8.075 N
Minimum force,
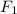 , required can be determined by;
, required can be determined by;
 =
=
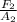
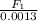 =
=
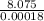
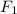 =
=
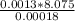
= 58.32
The minimum force that must be exerted on the piston is 58.32 N.