Question

Suppose the number of insect fragments in a chocolate bar follows a Poisson process with the expected number of fragments in a 200-gram chocolate bar being 10.2. 15. What is the expected number of insect fragments in 1/4 of a 200-gram chocolate bar? 16. What is the probability that you have to eat more than 10 grams of chocolate bar before nding your rst fragment? 17. What is the expected number of grams to be eaten before encountering the rst fragment?

Answer 1

a)The expected number of insect fragments in 1/4 of a 200-gram chocolate bar is 2.55

b)0.6004

c)19.607

Explanation:

Let X denotes the number of fragments in 200 gm chocolate bar with expected number of fragments 10.2

X ~ Poisson(A) where
`\lambda = (10.2)/(200) = 0.051`

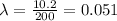
a)We are supposed to find the expected number of insect fragments in 1/4 of a 200-gram chocolate bar

`(1)/(4) * 200 = 50`

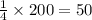
50 grams of bar contains expected fragments = \lambda x = 0.051 \times 50=2.55

So, the expected number of insect fragments in 1/4 of a 200-gram chocolate bar is 2.55

b) Now we are supposed to find the probability that you have to eat more than 10 grams of chocolate bar before ending your first fragment

Let X denotes the number of grams to be eaten before another fragment is detected.

`P(X>10)= e^(-\lambda * x)= e^(-0.051 * 10)= e^(-0.51)=0.6004`

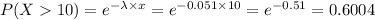
c)The expected number of grams to be eaten before encountering the first fragments :

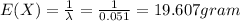`E(X)=(1)/(\lambda)=(1)/(0.051)=19.607 gram`s