Answer:
a)The expected number of insect fragments in 1/4 of a 200-gram chocolate bar is 2.55
b)0.6004
c)19.607
Explanation:
Let X denotes the number of fragments in 200 gm chocolate bar with expected number of fragments 10.2
X ~ Poisson(A) where
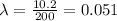
a)We are supposed to find the expected number of insect fragments in 1/4 of a 200-gram chocolate bar
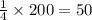
50 grams of bar contains expected fragments = \lambda x = 0.051 \times 50=2.55
So, the expected number of insect fragments in 1/4 of a 200-gram chocolate bar is 2.55
b) Now we are supposed to find the probability that you have to eat more than 10 grams of chocolate bar before ending your first fragment
Let X denotes the number of grams to be eaten before another fragment is detected.
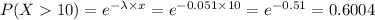
c)The expected number of grams to be eaten before encountering the first fragments :
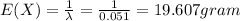 s
s