Answer:
The wood sample has an age of approximately 22800 years.
Step-by-step explanation:
The Becquerel (
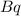 ) is a SI unit which describes radioactive activity related to decay of radioactive isotopes, which is equivalent to
) is a SI unit which describes radioactive activity related to decay of radioactive isotopes, which is equivalent to
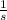 . The decay of radioactive isotope is described by the following ordinary differential equation:
. The decay of radioactive isotope is described by the following ordinary differential equation:
 (Eq. 1)
(Eq. 1)
Where:
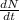 - Disintegration rate, measured in
- Disintegration rate, measured in
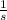 .
.
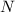 - Amount of remaining radioactive nuclei, dimensionless.
- Amount of remaining radioactive nuclei, dimensionless.
 - Time constant, measured in seconds.
- Time constant, measured in seconds.
By integration the solution of this differential equation is obtained:
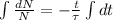
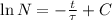
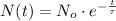 (Eq. 2)
(Eq. 2)
Let
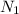 and
and
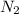 different disintegration rates for Carbon-14 samples, so that:
different disintegration rates for Carbon-14 samples, so that:
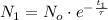 (Eq. 3)
(Eq. 3)
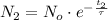 (Eq. 4)
(Eq. 4)
If we divide (Eq. 4) by (Eq. 3), then:

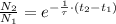 (Eq. 5)
(Eq. 5)
If
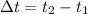 , we proceed to clear that variable:
, we proceed to clear that variable:
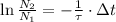
 (Eq. 6)
(Eq. 6)
Time constant is also a function of half-life (
 ), measured in seconds:
), measured in seconds:
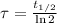
If
 ,
,
 and
and
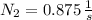 , the age of the wood sample is:
, the age of the wood sample is:
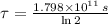
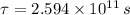
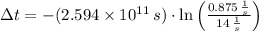
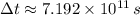
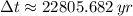
The wood sample has an age of approximately 22800 years.