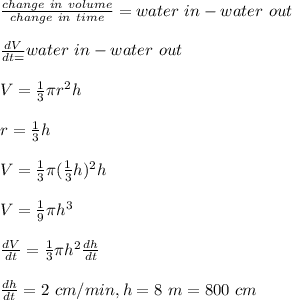Question

Consider a conical tank, where the height of the tank is 12 meters, and and the diameter of the tank at the top is 8 meters. Water is leaking out of the bottom of a conical tank at an constant rate of 20,000 LaTeX: \text{cm}^3 / \text{min}cm 3 / min. Water is also being pumped in to the tank at a constant unknown rate (call it LaTeX: kk). The water level is currently 8 meters high, and the water level is rising at a rate of 2 LaTeX: \text{cm} / \text{min}cm / min. Find the rate LaTeX: kk at which water is being pumped in to the tank.

Answer 1

The answer is below

Explanation:

The height of tank = 12 m = 1200 cm, the diameter of the tank = 8 meters, hence the radius of the tank = 8/2 = 4 m = 400 cm

Let h represent the water level = 8 m = 800 cm. The radius (r) of the water level at a height of 8 m is:

r/h = radius of tank/ height of tank

r/h = 400/1200

r = h/3

`(change\ in\ volume)/(change\ in \ time)=water\ in-water\ out\\ \\(dV)/(dt=) water\ in-water\ out\\\\V=(1)/(3)\pi r^2h\\ \\r=(1)/(3)h \\\\V=(1)/(3)\pi ((1)/(3)h )^2h\\\\V=(1)/(9) \pi h^3\\\\(dV)/(dt) =(1)/(3) \pi h^2(dh)/(dt)\\\\(dh)/(dt)=2\ cm/min,h=8\ m=800\ cm\\\\`

`(dV)/(dt) =(1)/(3) \pi (800)^2(2)=426666.7\ cm^3/min\\\\(dV)/(dt=) water\ in-water\ out\\\\426666.7\ cm^3/min= water\ in-water\ out\\\\426666.7\ cm^3/min= water\ in-20000\ cm/min\\ \\water\ in=426666.7\ cm^3/min+20000\ cm/min\\\\water\ in=446666.7 \ cm^3/min`