Question

1 point) The joint probability mass function of XX and YY is given by p(1,1)=0.1p(2,1)=0.1p(3,1)=0.05p(1,2)=0.05p(2,2)=0.3p(3,2)=0.1p(1,3)=0.1p(2,3)=0.05p(3,3)=0.15 p(1,1)=0.1p(1,2)=0.05p(1,3)=0.1p(2,1)=0.1p(2,2)=0.3p(2,3)=0.05p(3,1)=0.05p(3,2)=0.1p(3,3)=0.15 (a) Compute the conditional mass function of YY given X=3X=3: P(Y=1|X=3)=P(Y=1|X=3)= P(Y=2|X=3)=P(Y=2|X=3)= P(Y=3|X=3)=P(Y=3|X=3)= (b) Are XX and YY independent? (enter YES or NO) (c) Compute the following probabilities: P(X+Y>2)=P(X+Y>2)= P(XY=3)=P(XY=3)= P(XY>1)=P(XY>1)=

Answer 1

Explanation:

The given information shows that X and Y are two variables with joint probability distribution as follows:

X/Y 1 2 3 Total

1 0.1 0.05 0.1 0.25

2 0.1 0.3 0.05 0.45

3 0.05 0.1 0.15 0.3

Total 0.25 0.45 0.3 1.00

Thus, the required probability is:

`P(Y = 1|X=3) = (P(Y=1,X=3))/(P(X=3))`

`P(Y = 1|X=3) = (0.05)/(0.1)`

`P(Y = 1|X=3) =0.5`

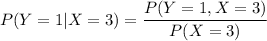
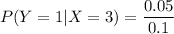
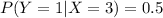
The calculated probability value of Y =1, given that X = 3 is 0.5

`P(Y = 2|X=3) = (P(Y=2,X=3))/(P(X=3))`

`P(Y = 2|X=3) = (0.1)/(0.1)`

`P(Y = 2|X=3) = 1.00`

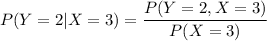
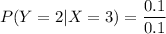
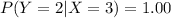
The calculated probability value of Y =2, given that X = 3 is 1.00

`P(Y = 3|X=3) = (P(Y=3,X=3))/(P(X=3))`

`P(Y = 3|X=3) = (0.15)/(0.1)`

`P(Y = 3|X=3) =1.5`

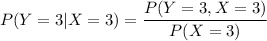
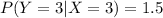
The calculated probability value of Y =3, given that X = 3 is 1.50

B.

From the joint probability distribution table, we can see that the probability value of the intersection X = 3 and Y = 3 is 1.50

i.e

P(X =3, Y =3) = 1.5

However;

the marginal probability of X = 0.3

the marginal probability of Y = 0.3

P(X =3)(Y=3) = 0.3 × 0.3 = 0.09

∴

≠ P(X =3)(Y=3)

Thus;

NO, the random variables X and Y are not independent.

C.

P(X+Y > 2) = P(X =2, Y = 1) + P( Y =2, X=1) + P(Y = 3, X= 1) + P( Y =2, X=2) +

P(Y =3, X=2) + P(Y =1, X =3) + P( Y =2, X =2) +P(Y =3, X =3)

P(X+Y > 2) = 0.1 + 0.05 + 0.1 + 0.3 + 0.05 + 0.05 + 0.1 + 0.15

P(X+Y > 2) = 0.9

P(XY =3) = P(X =2, Y =1 ) + P( Y =1 , X = 2)

P(XY =3) = 0.10 + 0.05

P(XY =3) = 0.15

P(XY > 1) = 0.1 + 0.05 + 0.1 + 0.1 + 0.3 + 0.05 + 0.05 + 0.1 + 0.15

P(XY > 1) = 1.00