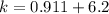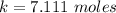Answer:
The value is
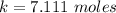
Step-by-step explanation:
Generally the reaction between ethylene and water vapor is
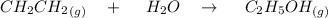
From the question the initial number of moles of ethylene is 33.mol
the initial number of moles of water vapor is 16.mol
So
At initial
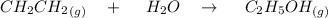
33.mol 16.mol 0 mols
Now at first equilibrium the number of moles of ethylene is 26.8mol
the number of moles of water vapor is 9.8mol
So the number of moles of ethanol is 33-26.8 = 6.2 mol
So at equilibrium
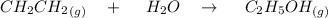
26.8mol 9.8mol 6.2 mol
Generally the equilibrium constant is mathematically represented as
![K = ([C_2H_5OH])/([CH_2CH_2] [H_2O])](https://img.qammunity.org/2021/formulas/chemistry/college/25wyxxfpy0peh5j30180aq48gnu237n4tc.png)
Here
![[C_2H_5OH]](https://img.qammunity.org/2021/formulas/chemistry/college/m523ayz5w0cvwzqps5o7c0vpmubdjhpkyr.png) is the concentration of ethanol which is mathematically represented as
is the concentration of ethanol which is mathematically represented as
![[C_2H_5OH] = (6.2 \ mol)/(100L)](https://img.qammunity.org/2021/formulas/chemistry/college/875yrpizsg3onq4cmm69iux4ww54hv7xpq.png)
=>
![[C_2H_5OH] = 0.062 mol/L](https://img.qammunity.org/2021/formulas/chemistry/college/torz7uy2wnqtb0mym7lbw3158e92vqqg0t.png)
Also
![[CH_2CH_2] = (26.8 \ mol)/(100L)](https://img.qammunity.org/2021/formulas/chemistry/college/b16mmqppw8u98fvv4ihigb33cfs9pk9sn2.png)
![[CH_2CH_2] = 0.268 mol/L](https://img.qammunity.org/2021/formulas/chemistry/college/dl4h91ivam4myyvz9qknf4i2vl3nkupflk.png)
Also
![[H_2O] = ( 9.8 \ mol)/(100L)](https://img.qammunity.org/2021/formulas/chemistry/college/98mu8dfqymuskffkb7gouj9wboxzbn7vll.png)
![[H_2O] = 0.098 mol/L](https://img.qammunity.org/2021/formulas/chemistry/college/kuxya2mshgpn3b7vscp8ab211y6d9c6b8x.png)
So

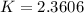
From the question we are told that 8 moles was added to ethylene
So volume of ethylene becomes 26.8 + 8 = 34.8 moles
So after the addition
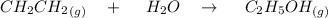
34.8mol 9.8mol 6.2 mol
At the second equilibrium
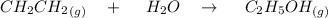
(34.8- z)mol (9.8-z)mol ( 6.2+z) mol
Generally the equilibrium constant is mathematically represented as
![K = ([C_2H_5OH])/([CH_2CH_2] [H_2O])](https://img.qammunity.org/2021/formulas/chemistry/college/25wyxxfpy0peh5j30180aq48gnu237n4tc.png)
Here
![[C_2H_5OH]](https://img.qammunity.org/2021/formulas/chemistry/college/m523ayz5w0cvwzqps5o7c0vpmubdjhpkyr.png) is now equal to
is now equal to
![[C_2H_5OH] = (6.2+z)/(100)](https://img.qammunity.org/2021/formulas/chemistry/college/iuvdkehhfsr51vlgh6c5xxzhrtrzkn69bu.png)
![[CH_2CH_2]= ( 34.8- z )/(100)](https://img.qammunity.org/2021/formulas/chemistry/college/fnt2xtxbcsjly68o8eu3u6yub936e6xmah.png)
![[CH_2CH_2]= ( 9.8-z )/(100)](https://img.qammunity.org/2021/formulas/chemistry/college/tcd9uymjey9png1mjrmpbpjmgdonl3l202.png)
So m
![2.3606 = ( (6.2+z)/(100))/([ (34.8- z )/(100)] [( 9.8-z )/(100)])](https://img.qammunity.org/2021/formulas/chemistry/college/73hzsslyk6ozedlaioi4vsaqop9u1p4fym.png)
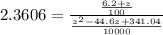
=>
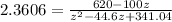
=>

=>

Multiply through by minus
=>
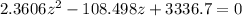
Solving this using quadratic equation
So
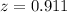
Hence the number of moles of ethanol present at the second equilibrium is