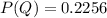Question

According to Masterfoods, the company that manufactures M&M’s, 12% of peanut M&M’s are brown, 15% are yellow, 12% are red, 23% are blue, 23% are orange and 15% are green. (Round your answers to 4 decimal places where possible) a. Compute the probability that a randomly selected peanut M&M is not green. 0.850 b. Compute the probability that a randomly selected peanut M&M is green or red. c. Compute the probability that two randomly selected peanut M&M’s are both red. d. If you randomly select two peanut M&M’s, compute that probability that neither of them are red e. If you randomly select two peanut M&M’s, compute that probability that at least one of them is red.

Answer 1

Complete question

The complete question is shown on the first uploaded image

Answer:

a

`y' = 0.85`

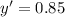
b

`P(J) = 0.27`

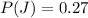
c

`P(R) = 0.0144`

d

`P(R') =  0.7744`

e

`P(Q) =0.2256`

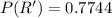
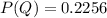
Explanation:

From the question we are told that

The proportion of M & M's that is brown is b = 0.12

The proportion of M & M's that is yellow is y = 0.15

The proportion of M & M's that is red is r = 0.12

The proportion of M & M's that is blue is b = 0.23

The proportion of M & M's that is orange is o = 0.23

The proportion of M & M's that is green is g = 0.15

Generally the probability that a random selected M&M is not yellow is

`y' =  1-y`

=>
`y' =  1-0.15`

=>
`y' = 0.85`

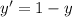
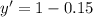
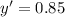
Generally the probability that a randomly selected peanut M&M isgreen or red is mathematically represented as

`P(J) =  g +  r`

=>
`P(J) =  0.15 + 0.12`

=>
`P(J) = 0.27`

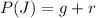
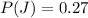
Generally the probability that two randomly selected peanut M&M’s are both red is mathematically represented as

`P(R) = r^2`

=>
`P(R) = 0.12^2`

=>
`P(R) = 0.0144`

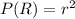
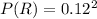
Generally if two two peanut M&M’s are selected the probability that neither of them are red is mathematically represented as

`P(R') =  (1 -r)^2`

=>
`P(R') =  (1 - 0.12)^2`

=>
`P(R') =  0.7744`

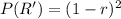
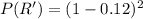
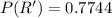
Generally if two two peanut M&M’s are selected the probability that at least one of them is red is mathematically represented as

`P(Q) =  1- P(R')`

=>
`P(Q) =  1- 0.7744`

=>
`P(Q) =0.2256`