Question

1. A gas pressure difference is applied to the legs of a U-tube manometer filled with a liquid with S = 1.5. The manometer reading is 286 mm. Find the pressure difference in kPa. (10 points)

2. Convert the pressure 2.5 psi into units of inches of mercury and feet of water (10 points)

Answer 1

1) The pressure difference is 4.207 kilopascals.

2) 2.5 pounds per square inch equals 5.093 inches of mercury and 5.768 feet of water.

Step-by-step explanation:

1) We can calculate the gas pressure difference from the U-tube manometer by using the following hydrostatic formula:

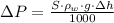`\Delta P = (S\cdot \rho_(w)\cdot g \cdot \Delta h)/(1000)` (Eq. 1)

Where:

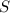`S` - Relative density, dimensionless.

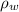`\rho_(w)` - Density of water, measured in kilograms per cubic meter.

`g` - Gravitational acceleration, measured in meters per square second.

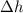`\Delta h` - Height difference in the U-tube manometer, measured in meters.

`\Delta P` - Gas pressure difference, measured in kilopascals.

If we know that
`S = 1.5`,
`\rho_(w) = 1000\,(kg)/(m^(3))`,
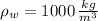`g = 9.807\,(m)/(s^(2))` and
`\Delta h = 0.286\,m`, then the pressure difference is:

`\Delta P = (1.5\cdot \left(1000\,(kg)/(m^(3)) \right)\cdot \left(9.807\,(m)/(s^(2)) \right)\cdot (0.286\,m))/(1000)`

`\Delta P = 4.207\,kPa`

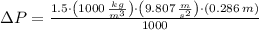
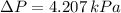
The pressure difference is 4.207 kilopascals.

2) From Physics we remember that a pound per square unit equals 2.036 inches of mercury and 2.307 feet of water and we must multiply the given pressure by corresponding conversion unit: (
`p = 2.5\,psi`)

`p = 2.5\,psi* 2.037\,(in\,Hg)/(psi)`

`p = 5.093\,in\,Hg`

`p = 2.5\,psi* 2.307\,(ft\,H_(2)O)/(psi)`

`p = 5.768\,ft\,H_(2)O`

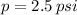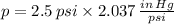
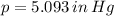
2.5 pounds per square inch equals 5.093 inches of mercury and 5.768 feet of water.