Answer:
a) Entonces, habrá una población de
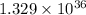 bacterias a las dos horas.
bacterias a las dos horas.
b) La población de bacterias será de 33554432 en 25 minutos.
Explanation:
a) De acuerdo con el enunciado, podemos apreciar una progresión geométrica, la cual está definida como:
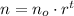 (Eq. 1)
(Eq. 1)
Donde:
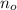 - Población inicial de bacterias, adimensional.
- Población inicial de bacterias, adimensional.
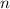 - Población actual de bacterias, adimensional.
- Población actual de bacterias, adimensional.
 - Tasa de reproducción de la población, adimensional.
- Tasa de reproducción de la población, adimensional.
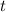 - Tiempo, medido en minutos.
- Tiempo, medido en minutos.
Si sabemos que
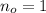 ,
,
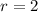 and
and
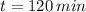 , entonces la población actual de las bacterias:
, entonces la población actual de las bacterias:
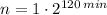
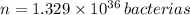
Entonces, habrá una población de
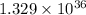 bacterias a las dos horas.
bacterias a las dos horas.
b) Si empleamos (Eq. 1) y asumimos que
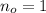 ,
,
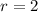 and
and
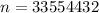 , entonces despejamos
, entonces despejamos
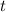 de la fórmula resultante:
de la fórmula resultante:
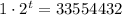
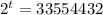
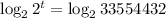
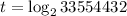
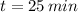
La población de bacterias será de 33554432 en 25 minutos.