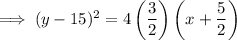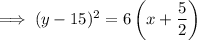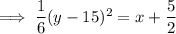Answer:
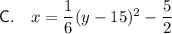
Explanation:
As the directrix is vertical, the parabola is sideways.
Conic form of a sideways parabola with a horizontal axis of symmetry:

- Vertex = (h, k)
- Focus = (h + p, k)
- Directrix: x = (h - p)
- Axis of symmetry: y = k
If p > 0, the parabola opens to the right, and if p < 0, the parabola opens to the left.
Given:
- Focus: (-1, 15)
- Directrix: x = -4
Therefore:
- k = 15
- h + p = -1
- h - p = -4
Add h + p = -1 to h - p = -4 to eliminate p:
⇒ 2h = -5
⇒ h = -5/2
⇒ p = 3/2
Substituting the found values into the formula: