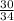Question

If tan(x)=3/5 and sin(x)>0, what is sin(2x)?

With STEPS PLEASE AND NO TROLLING.

Answer 1

i edited the answer. hope it helps. if it isn't ryt tell me plz

Answer 2

sin2x =
`(30)/(34)`

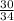
Explanation:

Given

tanx =
`(3)/(5)` =
`(opposite)/(adjacent)`

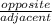
This is a right triangle with legs 3 and 5

Let the hypotenuse be h , then using Pythagoras' identity

h² = 3² + 5² = 9 + 25 = 34 ( take the square root of both sides )

h =
`√(34)`

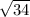
Thus

sinx =
`(opposite)/(hypotenuse)` =
`(3)/(√(34) )`

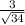
cosx =
`(adjacent)/(hypotenuse)` =
`(5)/(√(34) )`

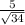
Hence

sin2x = 2sinxcosx = 2 ×
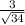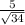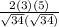`(3)/(√(34) )` ×
`(5)/(√(34) )` =
`(2(3)(5))/(√(34)(√(34)) )` =
`(30)/(34)`