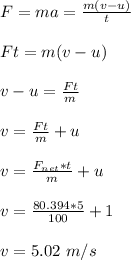Answer:
(a) The net force is 80.394 N
The acceleration of the crate is 0.804 m/s²
(b) the final velocity of the crate is 5.02 m/s
Step-by-step explanation:
Given;
mass of the crate, m = 100 kg
applied force, F = 250 N
angle of inclination, θ = 45°
coefficient of friction, μ = 0.12
Applied force in y-direction,

Applied force in x-direction,

The normal force is calculated as;
N + Fy -W = 0
N = W - Fy
N = (100 x 9.8) - 176.78
N = 980 - 176.78 = 803.22 N
The frictional force is given by;
Fk = μN
Fk = 0.12 x 803.22
Fk = 96.386 N
(a) The net force is given by;

Apply Newton's second law of motion;
F = ma

(b) the velocity of the crate after 5.0 s