In ΔOPQ, p = 180 inches, q = 120 inches and ∠O=171°. Find the length of o, to the nearest inch.

Question

asked Nov 27, 2021 163k views

2 Answers

Sachin Gorade · Answer 1 · 2021-12-02T14:28:58+0000

Given:

In ΔOPQ, p = 180 inches, q = 120 inches and ∠O=171°.

To find:

The length of o, to the nearest inch.

Solution:

According to cosine formula,

$a^2=b^2+c^2-2bc\cos A$

Using cosine formula in ΔOPQ, we get

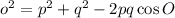
$o^2=p^2+q^2-2pq\cos O$

On substituting the values, we get

$o^2=(180)^2+(120)^2-2(180)(120)\cos (171^\circ)$

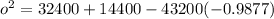
o^2=32400+14400-43200(-0.9877)

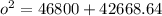
o^2=46800+42668.64

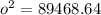
o^2=89468.64

Taking square root on both sides.

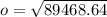
o=√(89468.64)

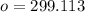
o=299.113

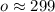
$o\approx 299$

Therefore, the length of o is about 299 inches.