Question

A cannon ball is shot horizontally off a 37.0 m cliff and lands a distance of 18.5 m

from the base of the cliff. Whall was the initial horizontal velocity of the cannon ball?

Answer 1

vₓ = 6.73 m/s

Step-by-step explanation:

• Assuming no other external influences than gravity, in the horizontal direction (which we make to coincide with the x- axis) , speed is constant, so, applying the definition of average velocity, we can write the following equation:

`v_(x) = (\Delta x)/(\Delta t) (1)`

• Now, in the vertical direction (coincident with the y- axis) , as both movements are independent each other, initial velocity is zero, so we can write the following equation for the vertical displacement:

`\Delta h = (1)/(2) * g * t^(2) (2)`

• where Δh = -37.0 m , g = -9.8 m/s2
• Solving (2) for t, we get:

`t = \sqrt{(2*\Delta h)/(g) } =\sqrt{(2*37.0m)/(9.8m/s2)} = 2.75 s (3)`

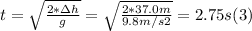
• Taking t₀ = 0, ⇒ Δt = t
• Replacing (3) in (1), we get:

`v_(x) = (\Delta x)/(\Delta t) = (x)/(t) = (18.5m)/(2.75s) = 6.73 m/s`

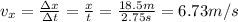
• As the horizontal velocity is constant, the initial horizontal velocity is just the average one, i.e., 6.73 m/s.