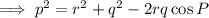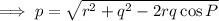Answer:
Law of Cosines, two sides, and the included angle are known
Explanation:
Law of Cosines
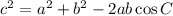
where:
- a, b and c are the sides
- C is the angle opposite side c
This rule can be used to find:
- an unknown side if 2 sides and the included angle is known.
- an unknown angle if all 3 sides are known.
Law of Sines

where:
- A, B and C are the angles
- a, b and c are the sides opposite the angles (a is opposite A, etc.)
This rule can be used to find:
- an unknown side when the opposite angle is known and another side and its opposite angle is known.
- an unknown angle when the opposite side is known and another angle and its opposite side is known.
Therefore, as sides r and q are given and the included angle ∠P is known, we can use the Law of Cosines to find side p: