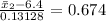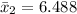Complete Question
Engineers must consider the breadths of male heads when designing helmets. The company researchers have determined that the population of potential clientele have head breadths that are normally distributed with a mean of 6.4-in and a standard deviation of 0.9-in.If you were to draw samples of size 47 from this population, in what range would you expect to find the middle 50% of most averages for the breadths of male heads in the sample
Answer:
The range is from
 to
to
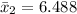
Explanation:
From the question we are told that
The mean is

The standard deviation
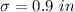
The sample size is n = 47
Generally the standard error is mathematically represented as

=>
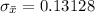
Generally the proportion where the middle 50% of most average for the breaths of male heads in the sample is mathematically evaluated as
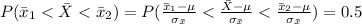
Generally
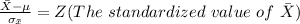
So
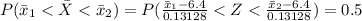
From the z table the z-score of 0.5 is
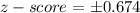
So
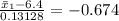

and