Question

The EPA wants to know the daily level of pollutant discharge in the manufacturing district in Pittsburgh for February 2005. The monitoring equipment reveals that the mean daily discharge per factory (calculated as total areal discharge divided by total areal factories) is 30.2 tons with a standard deviation of 9.1 tons. Construct a confidence interval for the true population mean of pollutant discharge using a 95% level of confidence.

Answer 1

The 95% confidence interval for the true population mean of pollutant discharge is (26.7 tons, 33.7 tons).

Explanation:

Let X represent the daily level of pollutant discharge in the manufacturing district in Pittsburgh.

The monitoring equipment reveals that for the 28 days of the February month

Mean daily discharge per factory, (
`\bar x`) = 30.2 tons

Standard deviation daily discharge per factory, (s) = 9.1 tons

Compute the critical value of t for 95% level of confidence and (n - 1 =) 27 degrees of freedom as follows:

`t_(0.05/2, 27)=2.052`

*Use a t-table.

Compute the 95% confidence interval for the true population mean of pollutant discharge as follows:

`CI=\bar x\pm t_(\alpha/2, (n-1))\cdot(s)/(√(n))`

`=30.2\pm 2.052*(9.1)/(√(28))\\\\=30.2\pm 3.53\\\\=(26.67, 33.73)\\\\\approx (26.7, 33.7)`

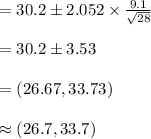
Thus, the 95% confidence interval for the true population mean of pollutant discharge is (26.7 tons, 33.7 tons).