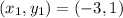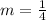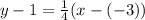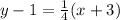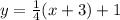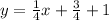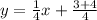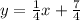Answer:
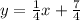
Explanation:
Given
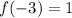
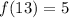
Required
Determine the linear function
A function is of the form:
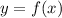
Writing the given parameters in (x,y) format, we have:
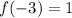 implies (-3,1)
implies (-3,1)
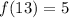 implies (13,5)
implies (13,5)
So, the x and y values are:
(-3,1) and (13,5)
i.e.
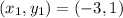
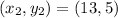
First, we need to determine the slope using:
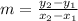
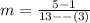
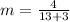
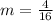
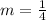
The equation is calculated as thus:
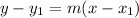
Where