Question

If a = (3-2√2) find the value of a4+ 1/a4 ​

Answer 1

1154

Explanation:

Perhaps the easiest way to evaluate this numerical expression is to let a calculator do it. Alternatively, we can compute the value from a +1/a.

__

expression

Consider the square of a +1/a:

(a +1/a)^2 = a^2 +2(a)(1/a) +1/a^2 = (a^2 +1/a^2) +2

This means ...

a^2 +1/a^2 = (a +1/a)^2 -2

Similarly, using a^2 for 'a' in the above, we have ...

a^4 +1/a^4 = (a^2 +1/a^2)^2 -2

numerical value

The value of a +1/a is ...

`a+(1)/(a)=3-2√(2)+(1)/(3-2√(2))=(3-2√(2))+(3+2√(2))/(3^2-(2√(2))^2)\\\\=(3-2√(2))+(3+2√(2))\\\\a+(1)/(a)=6`

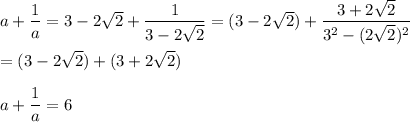
Then the value of a^2 +1/a^2 is 6^2 -2 = 34

and the value of a^4 +1/a^4 is 34^2 -2 = 1154