Question

Three people pull simultaneously on a stubborn donkey. Jack pulls directly ahead of the donkey with a force of 63.9 N63.9 N , Jill pulls with 79.1 N79.1 N in a direction 45° to the left, and Jane pulls in a direction 45° to the right with 183 N183 N . (Since the donkey is involved with such uncoordinated people, who can blame it for being stubborn?) Find the magnitude of the net force the people exert on the donkey.

Answer 1

a) F = (137.4 i ^ + 185 j ^) N

b) F = 230.2 N , θ = 53.5º

Step-by-step explanation:

In this exercise we ask to find the net force, for which we will define a coordinate system fix the donkey and use trigonometry to decompose the forces

Jack F₁ₓ = 63.9 N

Jill F₂ = 79.1 N with direction 45º to the left

cos (180 -45) = F₂ₓ / F₂

sin 135 =
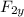`F_(2y)` / F₂

F₂ₓ = F₂ cos 135

F_{2y} = F₂ sin 135

F₂ₓ = 79.1 cos 135 = -55.9 N

F_{2y} = 79.1 sin 135 = 55.9 N

Jane F₃ = 183 N direction 45th to the right

cos 45 = F₃ₓ / F3

sin 45 = F_{3y} / F3

F₃ₓ = F₃ cos 45 = 183 cos 45

F_{₃y} = F₃ sin 45 = 183 sin 45

F₃ₓ = 129.4 N

F_{3y} = 129.4 N

we add each component of the force

Fₓ = F₁ₓ + F₂ₓ + F₃ₓ

Fₓ = 63.9 + (-55.9) + 129.4

Fₓ = 137.4 N

F_{y} = F_{2y} + F_{3y}

F_{2y} = 55.9 + 129.4

F_{2y} = 185.3 N

we can give the result of the forms

a) F = (137.4 i ^ + 185 j ^) N

b) in the form of module and angle

F = RA (Fₓ² + F_{y}²)

F = Ra (137² + 185²)

F = 230.2 N

tan θ = F_{y} / Fₓ

θ = tan⁻¹ F_{y} / Fₓ

θ = tan⁻¹ (185/137)

θ = 53.5º