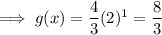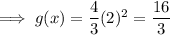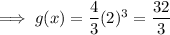Answer:
Given function:
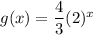
To find the y-intercept, input x = 0:
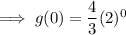
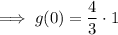
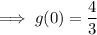
End behaviors:
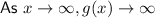
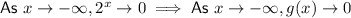
Therefore, y = 0 is an asymptote (the curve gets close to but never touches the x-axis).
To help graph accurately (rather than sketch), input other positive values of x as plot points for the curve: