This is an exercise in the law of Jackes Alejandro Charles.
To start solving this exercise, we obtain the following data:
Data:
- V₁ = 300 cm³
- T₁ = 300 k
- V₂ = ¿?
- T₂ = 600 km
If the temperature doubles the volume doubles; If the temperature is halved, the volume is halved.
"Mathematically this law expresses itself"
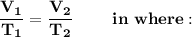
- V₁= Initial volume
- V₂ = Final volume
- T₁ = Initial temperature
- T₂ = Final temperature
We can also express it: V₁T₂=V₂T₁
Clear for "V₂":
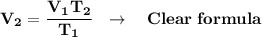
We clear our data in the formula:
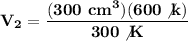
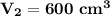
The new volume of the balloon will be 600 cm³.
