Question

X2 + 45x = -200 Using the quadratic formual and the discirimnat

Answer 1

Positive discriminant = 2 real solution

x= -5,-40

Explanation:

The discriminant is used to see how many solutions an equation has. If it is negative, the equation has no real solutions, if =0 the equation has 1, and if it is positive, the equation has two real solutions.

The discriminant is the part of the quadratic formula inside the square root:

`b^(2)-4ac`

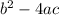
Every quadratic formula has the structure:

`ax^(2) +bx+c=0`

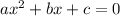
So first, in order to meet this structure we need to add 200 to both sides so the equation is equal to 0. This gives us:

`x^(2) +45x+200=0`

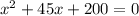
Our a=1, b=45 and c=200

Now we can substitute these values into the discriminant:

`(45)^(2) -4(1)(200)`

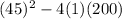
Solve:

`2025-800=1225`

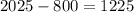
The discriminant is a positive number which means this equation will have 2 real solution. Now we just need to plug in our values into the quadratic formula to solve this equation. Quadratic formula:

`x=\frac{-+/-\sqrt{b^(2)-4ac} }{2a} \\x=(-45+/-√(1225) )/(2)`

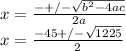
(Same discriminant value)

`x=(-45+/-35)/(2)`

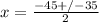
Now to find the two solutions, we use both signs in the equation. Solution 1:

`x=(-45+35)/(2)`

`x=(-10)/(2)=-5`

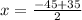
Our first solution is -5, now for the second:

`x=(-45-35)/(2)\\\\ x=(-80)/(2)=-40`

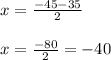
The two solution to this equation are -5 and -40.

Hope this helped!