Question

Find x. Give reasons to justify your solution. b Lines AB and CD are straight lines.

Answer 1

x is 28

Explanation:

When two lines intersected in a point, then they formed two pairs of vertically opposite angles. The vertically opposite angles are equal in measures

Let us solve our question

∵ AB and CD are straight lines intersected at O

∴ ∠AOC and ∠DOB are vertically opposite angles

∴ ∠AOD and ∠COB are vertically opposite angles

→ The vertically opposite angles are equal in measures

∴ m∠AOC = m∠DOB

∴ m∠COB = m∠AOD

→ ∠ COB is formed from ∠COE, ∠EOF, and ∠FOB

∵ m∠COB = m∠COE + m∠EOF + m∠FOB

∵ m∠COE = 3x, m∠EOF = x, m∠FOB = x + 12

∴ m∠COB = 3x + x + x + 12

→ Add the like terms

∴ m∠COB = 5x + 12

∵ m∠AOD = 152°

∵ m∠COB = m∠AOD

∴ 5x + 12 = 152

→ Subtract 12 from both sides

∴ 5x + 12 - 12 = 152 - 12

∴ 5x = 140

→ Divide both sides by 5

∴
`(5x)/(5)=(140)/(5)`

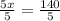
∴ x = 28

→ To justify the solution substitute x by 28 in m∠COB the answer must

be 152°

∵ m∠COB = 5x + 12

∵ x = 28

∴ m∠COB = 5(28) + 12

∴ m∠COB = 140 + 12

∴ m∠COB = 152°

∴ The value of x is correct