Question

In the diagram below, the radii of the two concentric circles are 3 centimeters and 7 centimeters, respectively.

What is the area of the shaded region?

Answer 1

Since the radii of the two concentric circles are 3 centimeters and 7 centimeters, the area of the shaded region is 40π square centimeters.

In Mathematics and Euclidean Geometry, the area of a circle can be calculated by using this mathematical equation (formula):

Area of a circle, A = π
`r^2`

Where:

r represents the radius of a circle.

By substituting the given parameters into the formula for the area of a circle, the area of the larger circle is given by;

Area of larger circle = π ×
`7^2`

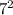
Area of larger circle = 49π square centimeters.

Area of smaller circle = π ×
`3^2`

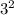
Area of smaller circle = 9π square centimeters.

Now, we can determine the area of the shaded region as follows;

Area of the shaded region = Area of larger circle - Area of smaller circle

Area of the shaded region = 49π - 9π

Area of the shaded region = 40π square centimeters.

Answer 2

125.6 cm²

Explanation:

Area of the shaded region = area of larger circle - area of the smaller circle

Area of the smaller circle = πr²

π = 3.14, r = 3 cm

Area of smaller circle = 3.14*3² = 3.14*9 = 28.26 cm²

Area of larger circle = πr²

π = 3.14, r = 7

Area of larger circle = 3.14*7² = 3.14*49 = 153.86 cm²

Area of the shaded region = 153.86 - 28.26 = 125.6 cm²