Question

A quadratic function has a line of symmetry at x = –3.5 and a zero at –9. What is the distance from the given zero to the line of symmetry? What is the other zero of the quadratic function?

Answer 1

Answer: A=0, B=6, C=4.

The axis of symmetry is x = ½

The smaller zero is -2

The larger zero is 3

Step-by-step explanation: Correct in edge 2020, the format makes it hard to find answers online but I just did the assignment

Answer 2

Given:

A quadratic function has a line of symmetry at x = –3.5 and a zero at –9.

To find:

The other zero.

Solution:

We know that, the line of symmetry divides the graph of quadratic function in two congruent parts. So, both zeroes are equidistant from the line of symmetry.

It means, line of symmetry passes through the mid point of both zeroes.

Let the other zero be x.

`-3.5=((-9)+x)/(2)`

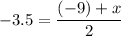
Multiply both sides by 2.

`-7=-9+x`

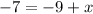
Add 9 on both sides.

`-7+9=-9+x+9`

`2=x`

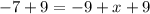
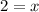
Therefore, the other zero of the quadratic function is 2.