Answer:
1). Length of diagonals = 52
2). m∠KON = 103°, m∠KMN = 45°
Explanation:
KLMN is a rectangle.
Diagonals KM and LN intersect at point O.
1). Since, diagonals of the rectangle equally bisect each other.
KM = 2(KO)
KM = 2(4y + 6)
And LN = 2(ON)
LN = 2(3y + 11)
Since, length of diagonals of a rectangle are equal in measure.
2(4y + 6) = 2(3y + 11)
4y + 6 = 3y + 11
4y - 3y = 11 - 6
y = 5
Therefore, length of diagonals = 2(3y + 11)
= 2(15 + 11)
= 52 units
2). m∠NKM = 32°
Since, m∠KNM = 90° [internal angle of a rectangle]
And diagonal LN bisects this angle,
m∠KNO = 45°
In ΔKNO,
m(∠NKM) + m(∠KNO) + m(KON) = 180°
32° + 45° + m∠KON = 180°
m∠KON = 180° - 77°
= 103°
Since, m∠KMN =
 (m∠LMN)
(m∠LMN)
m∠KMN =
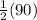 = 45°
= 45°