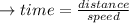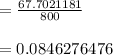Question

You're flying from Joint Base Lewis-McChord (JBLM) to an undisclosed location 201 km south and 194 km east. Mt. Rainier is located approximately 56 km east and 40 km south of JBLM. If you are flying at a constant speed of 800 km/hr, how long after you depart JBLM will you be the closest to Mt. Rainier?

Answer 1

The answer is "0.0846276476".

Explanation:

Let all the origin(0,0) of JBLM be

Let the y-axis be north along with the vector j unit.

But along the + ve x-axis is east, and all along with the vector unit i.

And at (194,-201) that undisclosed position is

Mt. Ris (56,-40) at

Let the moment it gets close to the Mt. rainier bet.

Oh, then,

If we know, the parallel to the direction from the point was its nearest one to a path to a point,

Calculating slope:

`\to m=(y_2-y_1)/(x_2-x_1)\\`

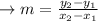
points: (0,0) and (194,-201)

`\to m=(-201 -0 )/(194-0)\\\\\to m=(-201)/(194)\\\\\to m=-1.03`

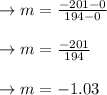
equation of the line:

`\to y= mx+c\\\\\to y= -1.03\ x+c`

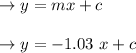
when the slope is perpendicular=
`-(1)/(m)`

`= - (1)/( -1.03)\\\\= (1)/( 1.03)\\\\= 0.97`

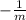
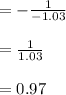
perpendicular equation:

`\to y-(-40)=0.97 * (x-56) \\\\\to y+40=0.97 * (x-56) \\\\`

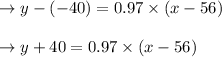
Going to solve both of the equations to have the intersection point,

We get to the intersect level in order to be at

(47.16,-48.5748)

so the distance from origin:

`= √((47.16^2+48.5748^2))\\\\= √(2224.0656 + 2359.5112)\\\\=√(4583.5768)\\\\=67.7021181`

`\to time =(distance )/(speed)`

`= (67.7021181)/(800)\\\\= 0.0846276476`