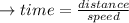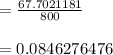Answer:
The answer is "0.0846276476".
Explanation:
Let all the origin(0,0) of JBLM be
Let the y-axis be north along with the vector j unit.
But along the + ve x-axis is east, and all along with the vector unit i.
And at (194,-201) that undisclosed position is
Mt. Ris (56,-40) at
Let the moment it gets close to the Mt. rainier bet.
Oh, then,
If we know, the parallel to the direction from the point was its nearest one to a path to a point,
Calculating slope:

points: (0,0) and (194,-201)

equation of the line:
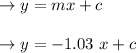
when the slope is perpendicular=

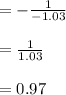
perpendicular equation:
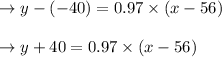
Going to solve both of the equations to have the intersection point,
We get to the intersect level in order to be at
(47.16,-48.5748)
so the distance from origin: