Question

During a soccer game, a goalie kicks a ball upward from the ground. The equation h(t)=-10t^2+40 represents the height of the ball above the ground in feet as a function of time in seconds. When the ball begins moving downward toward the ground, a player from the other team intercepts the ball with his chest 11 feet above the ground. How long after the goalie kicks the ball does the player intercept the ball?

Answer 1

3.98 seconds

Explanation:

The given relationship between height, in feet, and the time, in seconds, is

`h(t)=-10t^2+40`

`\Rightarrow t^2=(40-h(t))/(10)`

`\Rightarrow t= \pm√(4-0.1h(t))\cdots(i)`

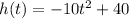
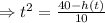
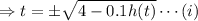
Let at time
`t_1`, the ball was at the goalie, so,
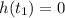`h(t_1)=0`, and at the time
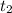`t_2`, the ball was intercepted, so,
`h(t_2)=11`.

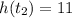Now, the time to reach the player after the goalie kicks the ball

`\Delta t=t_2-t_1`

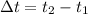
By using equation (i)

`\Delta t=(\pm√(4-0.1h(t_2)))-\left(\pm√(4-0.1h(t_1))\right)\cdots(ii)`

Now, at the highest point, the slope of the graph must be zero.

So,
`\frac {dh(t)}{dt}=0`

`\Rightarrow -20t=0`

`\Rightarrow t=0`

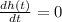
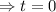
As at the highest point, the time is zero, to before reaching the highest point ( when kikes by the goalie,
`t_1`) take the time with the negative sign and after the highest point (when the ball intercepted,
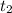`t_2`) take the positive sign.

So, from equation (ii) become.

`\Delta t=√(4-0.1* 11)-\left(-√(4-0.1* 0) \right)`

`=√(3.9)-(-\sqrt 4)`

`=1.98+2`

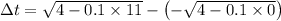
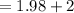
= 3.98 seconds

Hence, the time to reach the ball to the player after the goalie kicks the ball is 3.98 seconds.