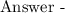
the question asks us to find the values of y.
the question can be solved as follows ~
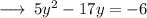
let's first convert the equation into its general formula , i.e. , ax² + bx + c = 0
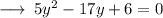
using splitting the middle term , let's find out the factors of the given equation ~
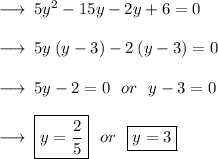
hope helpful ~