Answer:
B: a = 1, b= 7, c = -2
Explanation:
Quadratic Formula
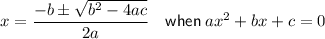
Given:
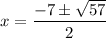
Comparing the terms of the given x-value with those of the quadratic formula:
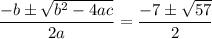
Therefore:
Using the found values of a and b to solve for c:
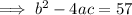
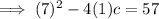
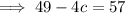
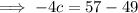

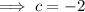
In summary: a = 1, b = 7, c = -2
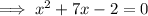
Therefore, option B is the correct solution.