Question

Determine what must be multiplied so that the expression below will have a common denominator. Use the backslash / to type in a fraction.

Answer 1

Multiply the first fraction by
`(x+4)/(x+4)`

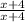
Multiply the second fraction by
`(x-4)/(x-4)`

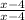
Explanation:

Given

`(4)/(x^2 - 16) + (3)/(x^2 + 8x + 16)`

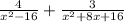
Required

Make the denominator equal

`(4)/(x^2 - 16) + (3)/(x^2 + 8x + 16)`

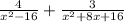
Factorize the denominator

`(4)/(x^2 - 4^2) + (3)/(x^2 + 4x + 4x+ 16)`

`(4)/((x - 4)(x + 4)) + (3)/((x+ 4)(x + 4))`

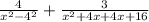
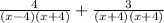
Multiply the first fraction by
`(x+4)/(x+4)`

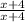
Multiply the second fraction by
`(x-4)/(x-4)`

`(x+4)/(x+4) * (4)/((x - 4)(x + 4)) + (3)/((x+ 4)(x + 4)) * (x-4)/(x-4)`

`(4(x + 4))/((x - 4)(x + 4)(x + 4)) + (3(x - 4))/((x+ 4)(x + 4)(x - 4)))`

`(4(x + 4))/((x^2 - 16)(x + 4)) + (3(x - 4))/((x^2 - 16)(x + 4)))`

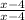
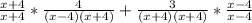
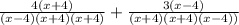
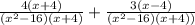
The expression now have the same denominator