You're very close. The answers you've selected are correct, but there's one third series that's also alternating. Choice C is also an answer due to the
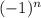 term.
term.
Any alternating series is in the form
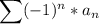 or
or
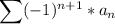 where
where
 is any sequence.
is any sequence.
Choice E comes close, but the 2n being the exponent means that we don't have alternating signs (positive, negative, positive negative, etc). Why is this? Well notice how 2n is even regardless of what integer n we pick. Raising any negative number to an even power results in a positive value.
Eg: (-7)^2 = 49 and (-3)^4 = 81
This means that all of the terms of sequence E are going to be positive. The terms do not bounce back and forth between positive and negative.
Put another way,

So
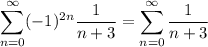
And it's why choice E is not one of the answers.
-------------------------
To summarize:
The 3 answers are A, C, and D