Question

I need help in finding numerical value please

Answer 1

Exact Answer:
`4√(2) - 3√(3)`

Approximate Answer: 0.46070182678574

Round the approximate value however you need to.

=================================================

Work Shown:

`C = √( B^2 + A^2 - 2BA)\\\\C = √( B^2 - 2BA + A^2)\\\\C = √( (B-A)^2 )\\\\C = -(B-A) \ \ \text{ see note below}\\\\C = -B+A\\\\C = A-B\\\\C = (A) - (B)\\\\`

`C = (√(2)+√(18)) - (√(3)+√(12))\\\\C = √(2)+√(18) - √(3)-√(12)\\\\C = √(2)+√(9*2) - √(3)-√(4*3)\\\\C = √(2)+√(9)*√(2) - √(3)-√(4)*√(3)\\\\C = √(2)+3√(2) - √(3)-2√(3)\\\\C = 4√(2) - 3√(3) \ \ \text{ ..... exact value}\\\\C \approx 0.46070182678574 \ \ \text{ ..... approximate value}`

-------------------

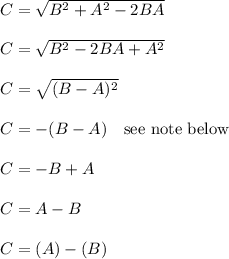
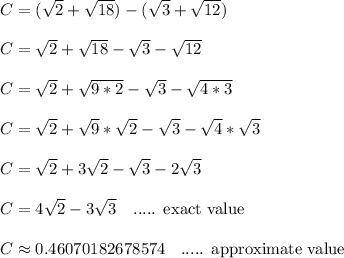
Note: The rule used here is

If x is positive then
`√(x^2) = x`

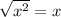
Or if x is negative, then
`√(x^2) = -x`

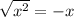
Since B-A = -0.4607 approximately, we will use the second version of the rule above.

Answer 2

Explanation:

`√(18)=√(2*3*3)=3√(2)`

`√(12)=√(2*2*3)=2√(3)`

`A=√(2)+√(18)\\\\=√(2)+3√(2)\\\\=(1+3)√(2)\\\\=4√(2)`

`B=√(3)+√(12)=√(3)+2√(3)\\\\ = (1+2)√(3)\\\\ = 3√(3)`

`\sqrt{B^(2)+A^(2)-2*B*A}=\sqrt{(B-A)^(2)}\\\\=B-A\\\\=3√(3)-4√(2)`

= 3* 1.732 - 4 *1.4142

= 5.196 - 5.6568

= -0.4608