Question

You have 500 meters of fencing with which to make two enclosures.

One enclosure will be in the shape of a square, and the other will have the shape of an isosceles right triangle. For example, the enclosures might look like this:

1) How long should the legs of the triangle be to minimize the combined area of the two enclosures?

Answer 1

The length of the legs of the triangle is approximately 86.85 meters

Explanation:

The requirement is to minimize the combined area of the two enclosures

The given parameters are;

The length of (perimeter) fencing available = 500 meters

The shape of the first enclosure = Square

The shape of the second enclosure = Triangle

The shape of the triangle = Isosceles right triangle

The area of the square = Side, S, squared = s²

The perimeter of the square = 4 × s

The area of the triangle = 1/2 × Base × Height = 1/2 × b × b= 1/2·b²

Where;

b = The lengths of the legs of the triangle

Given that the perimeter is 500 m, we have;

length of hypotenuse of triangle = √(b² + b²) =√(2·b²) = b·√2

∴ 500 - 4·s = b + b + b·√2 = 2·b + (√2)·b = b·(2 + √2)

b = (500 - 4·s)/(2 + √2)

∴ The area of the triangle = 1/2 × ((500 - 4·s)/(2 + √2))²

The area of the square + The area of the triangle = s² + 1/2 × ((500 - 4·s)/(2 + √2))²

At minimum value, we have;

d(s² + 1/2 × ((500 - 4·s)/(2 + √2))²/ds = 0, gives (Using online application)

`2\cdot \left (s - (8\cdot (125 - s))/(\left (2 + √(2) \right )) \right ) = 0`

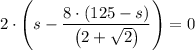
From which we have, s = 500/(7 + 2·√2)

Differentiating again gives;

`\frac{\mathrm{d} \left (2\cdot \left (s - (8\cdot (125 - s))/(\left (2 + √(2) \right )) \right ) \right ) }{\mathrm{d} x} = 26 - 16 \cdot √(2) \approx 3.37`

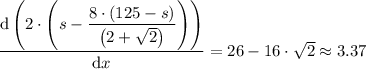
Therefore, the point is a local minimum and the length of the legs of the triangle should be given as follows;

The length of the legs of the triangle = b = (500 - 4·s)/(2 + √2) = (500 - 4*(500/(7 + 2*√2)))/(2 + √2) ≈ 86.85

The length of the legs of the triangle ≈ 86.85 meters.