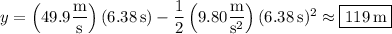Question

A baseball player hits a homerun, and the ball lands in the left field seats, which is 103m away from the point at which the ball was hit. The ball lands with a velocity of 20.5 m/s at an angle of 38 degrees below horizontal. Ignoring air resistance

(a) Find the initial velocity and the angle above horizontal with which the ball leaves the bat
(b) Find the height of the ball relatively to the ground.

Answer 1

(a) The ball has a final velocity vector

`\mathbf v_f=v_(x,f)\,\mathbf i+v_(y,f)\,\mathbf j`

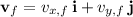
with horizontal and vertical components, respectively,

`v_(x,f)=\left(20.5(\rm m)/(\rm s)\right)\cos(-38^\circ)\approx16.2(\rm m)/(\rm s)`

`v_(y,f)=\left(20.5(\rm m)/(\rm s)\right)\sin(-38^\circ)\approx-12.6(\rm m)/(\rm s)`

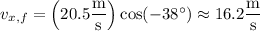
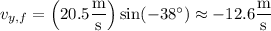
The horizontal component of the ball's velocity is constant throughout its trajectory, so
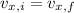`v_(x,i)=v_(x,f)`, and the horizontal distance x that it covers after time t is

`x=v_(x,i)t=v_(x,f)t`

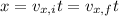
It lands 103 m away from where it's hit, so we can determine the time it it spends in the air:

`103\,\mathrm m=\left(16.2(\rm m)/(\rm s)\right)t\implies t\approx6.38\,\mathrm s`

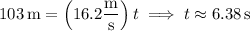
The vertical component of the ball's velocity at time t is

`v_(y,f)=v_(y,i)-gt`

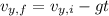
where g = 9.80 m/s² is the magnitude of the acceleration due to gravity. Solve for the vertical component of the initial velocity:

`-12.6(\rm m)/(\rm s)=v_(y,i)-\left(9.80(\rm m)/(\mathrm s^2)\right)(6.38\,\mathrm s)\implies v_(y,i)\approx49.9(\rm m)/(\rm s)`

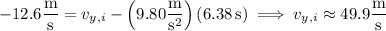
So, the initial velocity vector is

`\mathbf v_i=v_(x,i)\,\mathbf i+v_(y,i)\,\mathbf j=\left(16.2(\rm m)/(\rm s)\right)\,\mathbf i+\left(49.9(\rm m)/(\rm s)\right)\,\mathbf j`

which carries an initial speed of

`\|\mathbf v_i\|=\sqrt{{v_(x,i)}^2+{v_(y,i)}^2}\approx\boxed{52.4(\rm m)/(\rm s)}`

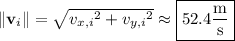
and direction θ such that

`\tan\theta=(v_(y,i))/(v_(x,i))\implies\theta\approx\boxed{72.0^\circ}`

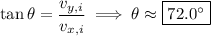
(b) I assume you're supposed to find the height of the ball when it lands in the seats. The ball's height y at time t is

`y=v_(y,i)t-\frac12gt^2`

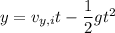
so that when it lands in the seats at t ≈ 6.38 s, it has a height of

`y=\left(49.9(\rm m)/(\rm s)\right)(6.38\,\mathrm s)-\frac12\left(9.80(\rm m)/(\mathrm s^2)\right)(6.38\,\mathrm s)^2\approx\boxed{119\,\mathrm m}`