Question

Alex is having a problem with spiders in his house. He proclaimed, “Every time I catch one spider, the number of remaining spiders doubles!” If there are now 194 spiders in Alex’s house, how many spiders were in his house before he caught the last 2 spiders?

a. 49
b. 50
c.52
d. 97

Answer 1

the answer is 50, or B.

Explanation:

Answer 2

B.

Explanation:

Let's write an equation that expresses the relationship.

Let s denote the amount of spiders.

We know that every time Alex catches one spider, the remaining population doubles.

So, if s represent the population of spiders, if Alex catches 1, then the population will become (s-1).

However, for every catch, the population doubles, so, the new population will be 2(s-1).

Therefore, we can write the following equation:

`s_n=2(s_o-1)`

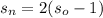
Where s_n represents the new population and s_o represents the original population.

We know that there are now 194 spiders in Alex's house. We want to find the number of spiders in his house before he caught the last 2 spiders. So, let's solve for s_o twice.

Substitute 194 for s_n. Solve for s_o:

`194=2(s_o-1)`

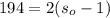
Divide by 2:

`97=s_o-1\\\Rightarrow s_o=98`

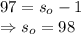
Therefore, before catching the last spider, there were 98 spiders.

So, to find the number of spiders before the last 2, we will solve for s_0 again. This time, we will use 98 for s_n. So:

`98=2(s_0-1)`

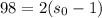
Solve for s_o:

`\Rightarrow 49=s_o-1\\\Rightarrow s_o=50`

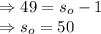
Therefore, there were 50 spiders in Alex's house before he caught the last 2 spiders given that the current population is 194 spiders.

Our answer is B.

Edit: Typo