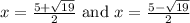2 Answers

Calaway · Answer 1 · 2021-09-30T17:15:45+0000

Answer:

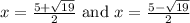
$x=(5+√(19))/(2)\text{ and } x=(5-√(19))/(2)$

Explanation:

If we have the standard form
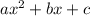ax^2+bx+c , then we can use the quadratic formula:

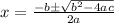
$x=(-b\pm√(b^2-4ac))/(2a)$

First, let's identify our coefficients. We have
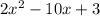2x^2-10x+3 .

This can be rewritten as
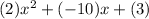(2)x^2+(-10)x+(3) .

Therefore, a=2, b=-10, and c=3.

Substitute these values into the quadratic formula. This yields:

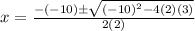
$x=(-(-10)\pm√((-10)^2-4(2)(3)))/(2(2))$

From here, simplify. Evaluate the expression under the square root:

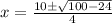
$x=(10\pm√(100-24))/(4)$

Evaluate:

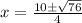
$x=(10\pm√(76))/(4)$

Note that:

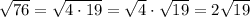
$√(76)=√(4\cdot 19)=√(4)\cdot√(19)=2√(19)$

Therefore:

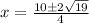
$x=(10\pm2√(19))/(4)$

We can factor out a 2 from both the numerator and the denominator:

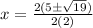
$x=(2(5\pm√(19)))/(2(2))$

Simplify:

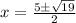
$x=(5\pm√(19))/(2)$

Therefore, our roots are:

$x=(5+√(19))/(2)\text{ and } x=(5-√(19))/(2)$

Please log in or register to add a comment.