Answer:

Explanation:
If we have the standard form
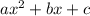 , then we can use the quadratic formula:
, then we can use the quadratic formula:
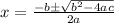
First, let's identify our coefficients. We have
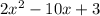 .
.
This can be rewritten as
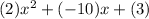 .
.
Therefore, a=2, b=-10, and c=3.
Substitute these values into the quadratic formula. This yields:
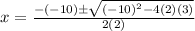
From here, simplify. Evaluate the expression under the square root:
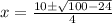
Evaluate:
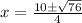
Note that:
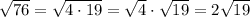
Therefore:
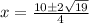
We can factor out a 2 from both the numerator and the denominator:

Simplify:
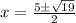
Therefore, our roots are:
